X-ray diffraction
This is a template which you can use to help get you started on the wiki submission. It is just intended as a guide and you may modify the structure to suit your project.
Contributors
- Jacob Edginton - Department of Physics (student partner) - Term 1 2021
- Hans Lee - Department of Physics (student partner) - Term 1 2021
- Benjamin Smith - Department of Mathematics (student partner) - Term 1 2021
- Ziang Yan - Department of Mathematics (student partner) - Term 1 2021
- Jonathan Rackham, Department of Materials. Staff partner from October 2021.
Aims & Learning Outcomes
- Explain the motivation for your visualisation.
- Introduce the subject of your visualisation.
- Which module and year is it intended for and which setting (lecture or self study)?
This visualisation would be used as teaching tools in MATE50005 (Materials Characterisation, second year undergraduate) lectures as well as self-study tools in lab sessions. It will also be useful in the MATE70001 module (MSc Characterisation course).
After using this visualisation, students will be able to:
- qualitatively describe the relationship between direct and reciprocal lattices.
- discuss the features of reciprocal space and how they relate to a crystal’s structure.
- relate the motion of a diffractometer to that of the scattering vector through reciprocal space.
- evaluate the effect of experimental conditions on the diffraction patterns obtained.
Design Overview
The design was split up into four main parts: Fourier transforms, diffraction patterns, reciprocal space, and the Ewald's sphere. The visualisations are shown graphically on the right.
Fourier Transforms
Fourier transform are the key mathematical framework for all of crystal X-ray diffraction theory. The Fourier visualisation shows two graphs: a function in the real domain, and the Fourier Transform of that function in the conjugate domain. The user is given control over an adjustable parameter in the function, for instance, for the Gaussian example, the user can control the width. If the play animation button is pressed, this parameter will be continuously varied such that the two graphs move in real time. The user is also given a rest button to return to the original conditions. A feedback button is available so that the design can be further improved. It can be seen that on the left side of the visualisation, there is written text and mathematical formulae that give an explanation of what the user is seeing graphically.
The main goal of this visualisation was to give the user an intuitive understanding of Fourier transformations, without having to rely on solely mathematics. The functions most relevant to the materials course were created in the visualisation: the Gaussian, the Top Hat function, a sinusoid, the Dirac delta, and the Dirac comb [more images to be added].
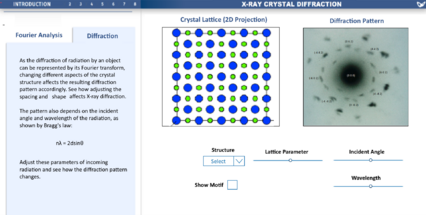
Diffraction Patterns
This section of the visualisation aimed to connect the geometry of the lattice of a crystal to the expected diffraction pattern if X-rays were incident. The user can control the type of lattice: rock salt, titanium, alumina, etc. Each type of lattice will have a different diffraction pattern based on its geometry. The user has control over three main parameters: the incident wavelength, the incident angle, and a lattice parameter corresponding to how spaced out each lattice point is.
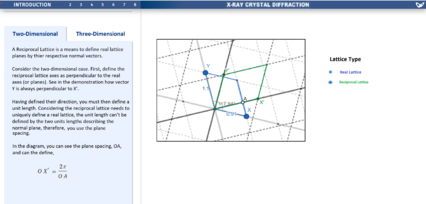
Reciprocal Space
One of the main theoretical techniques of X-ray crystal diffraction is to work in the reciprocal space - the conjugate domain and Fourier transform of real space. The real and reciprocal lattices are overlaid onto each other. A unit cell of the real space is shown in blue, and a unit cell of the reciprocal space is shown in green. The user can click the toggle points (labelled x and y) and move around the real lattice unit cell, then see what the subsequent reciprocal lattice unit cell looks like.
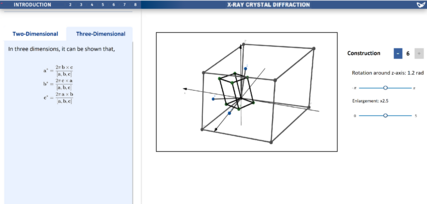
This concept was extended into 3D. A full 3D unit cell can be seen in both real and reciprocal space. As before, by clicking and moving toggle points, the user can change the size and shape of the real space unit cell, then see the resulting reciprocal space lattice cell. Moreover, the user has the ability to see how many vectors are shown: by adding or substracting on the constructions button, the number of vectors is varied. An enlargement factor can also be applied to the real lattice. Finally, the user has the ability to rotate the unit cell.
Ewald's Sphere
The Ewald's sphere is a construction in reciprocal space used to see if the elastic scattering condition of diffraction is met. The sphere is extended from an arbitrary lattice point, and has a radius equal to the magnitude of the wave vector (the reciprocal of wavelength). If two scattering vectors, k_i and k_f can connect two lattice points that intersect the sphere, than a diffraction will occur. The user has the option to toggle two different spheres, and can alter the magnitude of k_i.
Design Justification
Assessment Criteria
- List your cohort's assessment criteria. You may want to number the assessment criteria so you can refer to them easily later.
Education Design
- What Methods were considered to convey concepts?
- Design progression, key choices with justifications.
- How has feedback been incorporated.
Graphical Design
- How were accessibility issues considered?
- How was space used effectively?
- Design progression, key choices with justifications.
- How has feedback been incorporated.
- How is the design intuitive?
Interaction Design
- Choice of interactive element(s) that fit in organically with the visualisation [inspiration of choice might be from lecture/in-class activity or other sources] - Sliders/Buttons/Cursor (hover/click).
- Keeping accessibility of interactive elements in mind during design phase.
- Design progression, key choices with justifications.
- How has feedback been incorporated.
Progress and Future Work
- Is the design finalised?
- Which pages have been uploaded to website?
- Any ideas for future improvements.
Links
- Link to GitHub repository for code in development:
- Link to visualisation on ImpVis website (when uploaded):
- Link to Collection on ImpVis website (when created):
- Any other links to resources (Miro boards / notes pages / Google Docs etc):