Mathematical induction games
This is a template which you can use to help get you started on the wiki submission. It is just intended as a guide and you may modify the structure to suit your project.
Contributors
- Zerui Qian, Department of Physics, Student partner from October 2021
- Kelly Chang, Department of Medical Biosciences, Student partner from October 2021
- Max Bingham, Department of Physics, Student partner from October 2021
- Deniz Aydin, Department of Mathematics, Student partner from October 2021
- Mark Wheelhouse, Department of Computing. Staff partner from October 2021.
Staff Partner's Brief
1. Visualising "The Game of Frogs"
This is a thought experiment to get students thinking about Mathematical Induction. We would like to have a visualisation for this little game that will allow the students to experiment with the idea (number of frogs, starting speeds, etc).
The core learning outcome here is that a student should be able to provide an inductive argument to answer why all of the frogs will eventually fall off of the plank.
2. Visualising "The beetle and the cactus".
This is a thought experiment to get students thinking about Mathematical Induction. We would like to have a visualisation for this scenario that will allow the students to experiment with the idea (e.g. initial cactus set-up and beetle's rules). The core learning outcome here is that a student should be able to provide an inductive argument to show why the beetle can (and will) eventually consume the whole cactus. This thought experiment has also been referred to as "Hercules and the Hydra" and has an existing online visualisation.
I'd be happy with the students only tackling one of these two visualisations (not that I would be unhappy if they did both! - Mark
Aims & Learning Outcomes
- Explain the motivation for your visualisation.
- Introduce the subject of your visualisation.
- Which module and year is it intended for and which setting (lecture or self study)?
- List learning outcomes. E.g.: "After using this visualisation, students should be able to explain that..."
These two game visualisations will be shown during a lecture of COMP400018 - Discrete Mathematics, Logic and Reasoning. They will also be available for self-study so that students can validate what we have discussed in the lecture.
The two thought experiments are intended as playgrounds for developing an intuition for mathematical induction. Mathematical Induction is a technique for proving statements about a class of mathematical objects. The core idea is that if a statement is true for the first object in a sequence, and it being true for one object means that it is true for the next, then the statement must be true for all objects in the sequence. This can later be generalised to "structural induction", where the objects need not form a linear sequence but instead can be a part of any recursively defined structure, such as a tree.
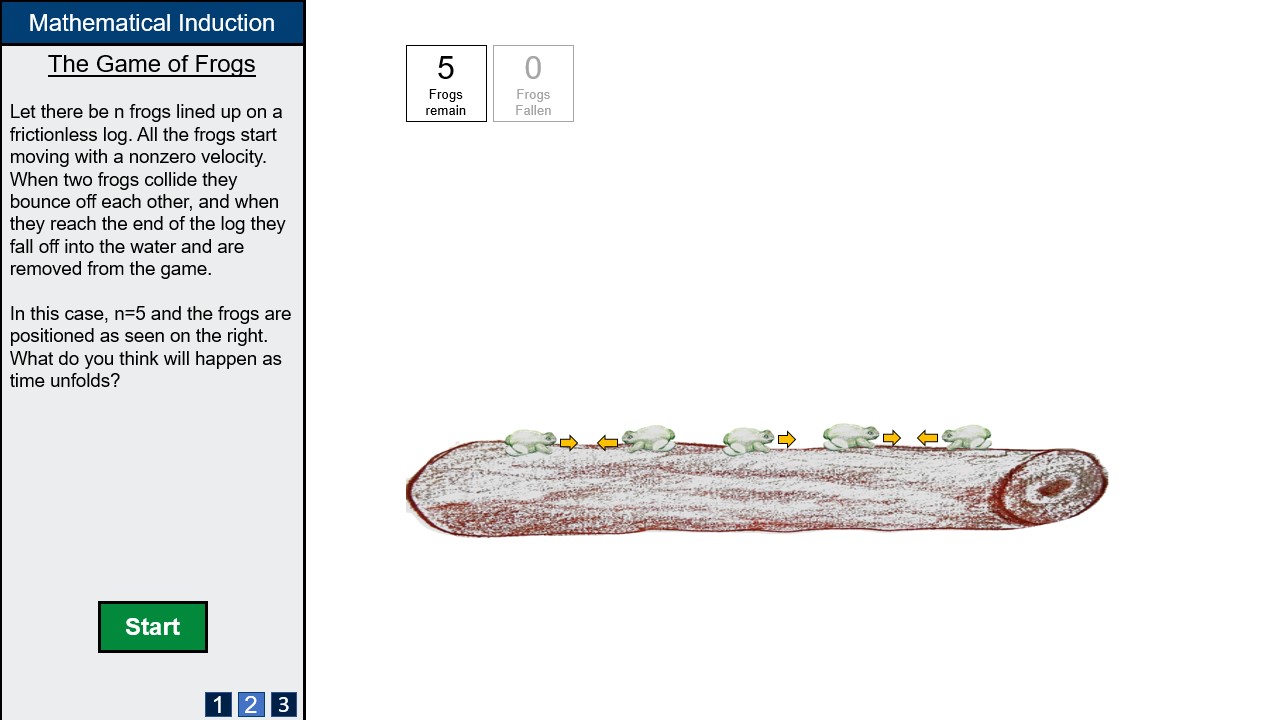
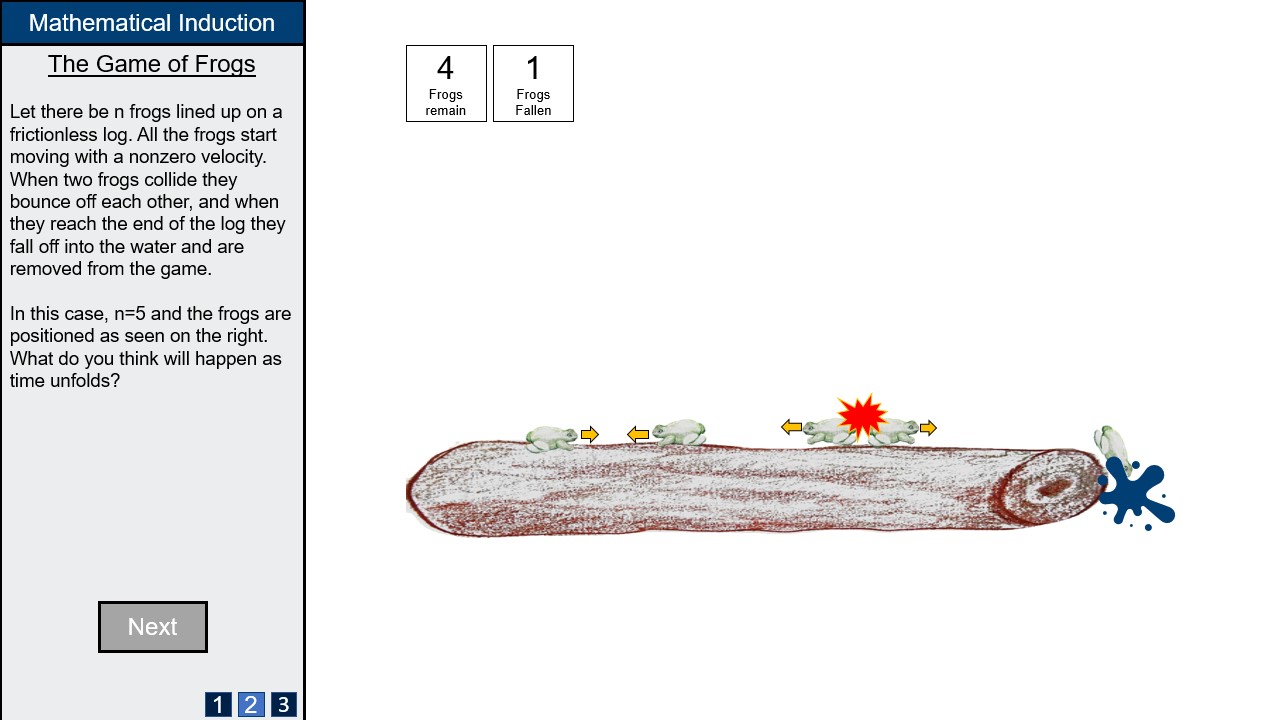
The first thought experiment is "The Game of Frogs", where n frogs slide back and forth on a 1-dimensional frictionless log. If two frogs collide, they bounce off eachother, and if they reach the end of the log they fall into the water and are removed from the game. It seems obvious that each frog must eventually fall into the water, but how can one prove this? After the lecture, the students should be able to provide such an inductive argument.
The second is "The Beetle and the Cactus". A beetle is attempting to eat a cactus which has a tree structure, where every segment can have other segments branching off of it. When it eats one of the outermost "leaf" segments the segment immedietly before it gets duplicated, along with every one of it's descendents. The question is whether or not the beetle can finish off the whole cactus. At first the cactus appears to grow exponentially making the task seem impossible, but the surprising fact is that not only can the beetle eat the whole cactus regardless of the starting configuration, it cannot be avoided so long as it keeps eating. The inductive argument here is more complicated, as the cactus can get bigger before it gets smaller. Because of this a a complete proof is not expected from the students, but it would be nice for them to be able to describe a rough overview of how such an argument would work.
For our visualisation, Mark has stated that it is not strictly necessary for the inductive arguments to be explained within the visualisation for them to be of use in his lecture. The main intent is for the visualisation to make the abstract thought experiments more real for the students to play with and the teaching will be done around them. Our designs will at least have self contained instructions for use, but we may consider including an overview of the inductive arguments.
Design Overview
We provide:
- A blueprint for a visualisation of "The Game of Frogs", suitable for use in lectures or as a self-contained learning tool. Educational, Graphical, and Interaction design factors have been considered.
- A javascript prototype for "The Beetle and the Cactus" tackling some of the technical problems involved in visualising this thought experiment.
The Game of Frogs
In The Game of Frogs, you swim or you die.
The Beetle and the Cactus
(Note: this link is live so functionality may break or change as I work on it. Reported not to work on some (Kelly's) browsers, should be fine on mobile now though)
Click on the leaf (pink) segments and watch the magic! Code can be seen by clicking the button in the top right.
Design Justification
Education Design
Though this was not a requirement in the brief, I felt as though it was necessary to provide context for why this topic matters in computer science. The explanation here would have been totally different if this was for a mathematics course, but I thought computing students would like to have the direct connection to computer programs explained. The decisions on what variables the user should control and what should be emphasized was also based on the educational context.
I would not say our visualisation alone fits the learning outcome specified in the brief as we did not get on to explaining the inductive argument, but I think this isn't so bad as it is intended to be a tool used alongside lectures to get the students thinking about how they would construct such an argument themselves. If we straight up told them the answer there wouldn't be much point in the interactive visualisation. However, an extra page detailing the argument is listed in potential future work.
Graphical Design
<remove this section when ready>
Talk about:
- Familiar icons
- colour scheme (based on Imperial brand colours)
- Use of space (text panel, why the sliders are vertical)
- How all the transitions are going to be smoothed
- Arrows change colour and size to convey velocity
</remove this section when ready>
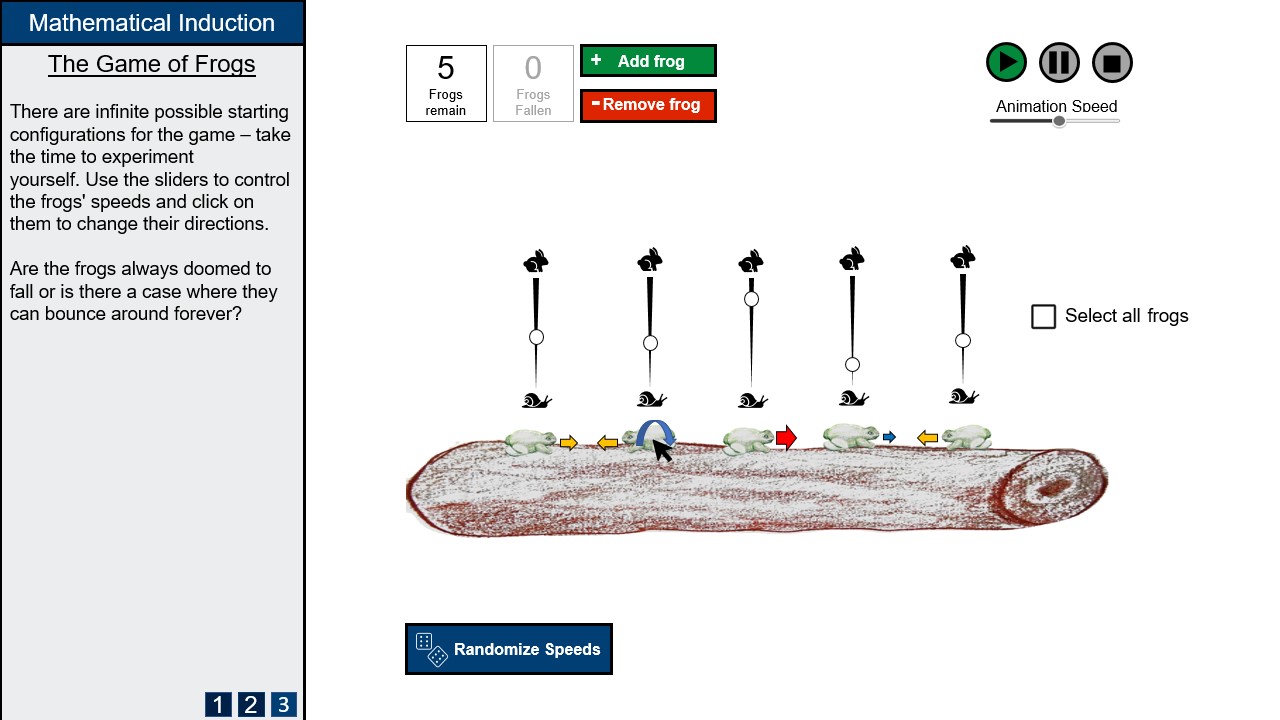
A key part of the design process was to have the fairly bare-bones concept of the mathematical problem appear more familiar to the user, in order to keep them passively engaged. Given the theme of animals, we thought a nice touch would be to include hare/snail symbols to indicate the speeds of the frogs in motion.
The red (wood), green (frog), and blue (water) colour scheme of the game lent itself well to the use of Imperial's own colour scheme to use in our UI. We felt this choice would look clear, in its simplicity, as well as be appropriate as an ImpVis visualisation.
We wanted the configuration of the game to be highly interactive for the user; enabling them to customise the speeds of the frogs with sliders allows them to get their hands on the problem at hand in an engaging way. By implementing vertical sliders we simultaneously provide this option to the user, and take up dead space caused by the one-dimensional aspect of the visualisation.
To keep from the visualisation feeling plain, one possibly feature of an implementation of this design could be a page transition in which the log, frogs, et al are dropped onto the screen (featuring water) at the start of a new page, and washed away by a stream at the end of one.
In keeping with mathematical tradition, the velocities of the frogs are indicated by vectors, this makes it clear to the user what the current behaviour of each element of the visualisation is. In an extreme case of many frogs being hard to keep track of, we employ a colour scheme to indicate the parity (direction) of their motion.
Interaction Design
In the main visualisation, buttons that start, pause, and reset the game are located at the upper left corner of the visualisation section. All buttons have icons, and in many cases these are so universal and familiar that text labels are not necessary. Buttons that cannot be interacted with at the current moment are "grayed out". Otherwise all buttons are colour-coded: yellow for pause, red for reset, green and red for adding and removing frogs.
We had much discussion about what parameters the user need to change as being able to control every detail could get overwhelming. We decided on these:
Number of Frogs
A frog counter is located at the upper left corner of the visualisation section. The number of frogs on the log, and number of frogs fallen off the log are shown, though the latter is greyed out while the simulation is not running as it conveys no useful information at that point. Even though you can infer the number of frogs remaining by looking at the image we still believe it is key information that needs to be emphasized as it is the core of the inductive argument. Users can control the number of frogs by clicking add and remove frog buttons, or typing in a number directly into the box if they wish to save time. A limit on the number of frogs will likely be needed but the exact number will be constrained by technical limitations.
Frog Velocities
The velocity of each individual frog can be changed by varying the slider above it. Sliders are ideal for this task as they are good for variables where full precision is not necessary. To make the purpose of these sliders intuitive, snail and hare icons are shown and the slider body gets thicker towards the top, indicating a rise in intensity as the slider goes up. With many frogs changing the velocities one by one is annoying so a button is provided to randomize all of them to get a varied spread of speeds without taking too long.
In addition, clicking on the frog will flip its direction. Hovering over a frog will show a blue circular arrow in order to make this obvious before the user does it.
Beetle and Cactus
The Beetle and Cactus prototype is intended more as a technical demonstration that a full design, but there are still some design decisions that go into it. The cactus itself is based on the prickly pear plant, as it the desired node-tree structure. This also makes the colour scheme very contrasting with the green body nodes and the pink clickable edge nodes.
The main thing the prototype does is provide a solution to the problem of displaying the full cactus and animating it's growth. Each of the descendants of a node are evenly spread out (by angle) around it, and when a node is removed the duplication of it's parent is smoothly animated with transparency so the user can clearly see what is being changed. An animation speed slider is provided so they can speed it up if they just wish to click through the entire cactus.
The starting cactus is chosen to be large enough for it to grow a fair amount as it gets eaten, but still be relatively quick to beat as slightly larger cacti get out of hand very fast! When there is no more cactus the following message is displayed:
The cactus is defeated! But now the beetle will starve - could it have sustained itself forever?
This poses an extra (impossible) challenge to the user and attempting it will force them to think about why the cactus will run out rather than just mindlessly clicking through it.
Further goals for this project could be an "auto" button that would eat away the cactus without user input, and more variance/choice in the inital configuration.
Progress and Future Work
- Is the design finalised?
No, it is a draft.
However further work could be including an explanation of the inductive arguments, and incorporating the beetle and cactus demonstration into the broader design with it's own introduction.